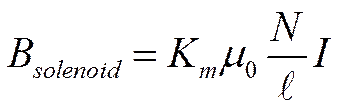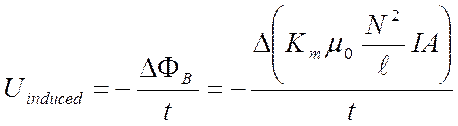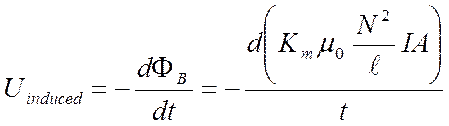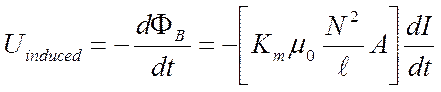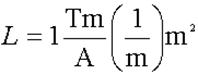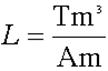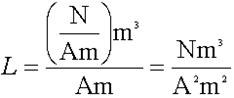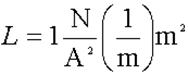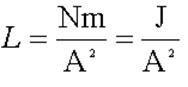DAY 20

Summary of Topics Covered in Today’s Lecture
NOTE – THIS PAGE USES SOME ANIMATION, AND CONTAINS A SUB-PAGE.
IT WILL NOT PRINT VERY WELL.

Mechanical Oscillations and Sound Waves

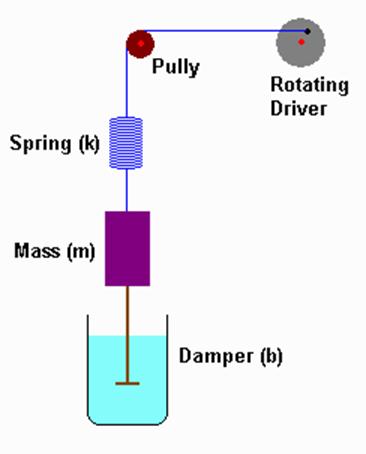A mechanical oscillator consists of a spring, a mass that oscillates, a damper, and a driving force. These are the components of any mechanically oscillating system.

If we look at this system from an energy standpoint, we see that each component plays a distinct role:

· The driver puts energy into the system.

· The spring stores energy in the form of elastic potential energy. The spring stores the greatest energy when the mass is not moving.

· The mass stores energy in the form of kinetic energy. The mass contains the greatest energy when it is moving at maximum speed.

· The damper takes the energy in the system and turns it into heat.

Thus a mechanical oscillator consists of a driver that putting energy into the system, energy oscillating between elastic potential energy and kinetic energy, and energy leaving the system via heat through the damper.

If the oscillator is in a medium that will support sound waves, such as air, the oscillating mass pushes the air back & forth, serving as a source for sound waves. The sound waves radiate out from the oscillator, taking some of the energy of the oscillator with them (thus the air acts as a damping mechanism, too).

http://www.kettering.edu/~drussell/Demos/rad2/mdq.html

This animation shows sound waves radiating outward from an oscillating mass. Note that in this animation the oscillating mass moves horizontally.

All of these are present in something that makes sound, such as a violin string. The string has mass. The string also has elasticity (which plays the role of the spring). Air and various frictions within the instrument play the role of a damper. The bow that is drawn across the violin string is the driver. When a musician draws the bow across the string, he drives the system to oscillate. The oscillations of the string serve as the source of sound waves which radiate outward from the instrument.

Electromagnetic Oscillations and Waves

What about an electrical equivalent of this mechanical oscillation that serves as a source for mechanical (sound) waves? Can we have electrical or magnetic oscillations that serve as a source for electrical or magnetic waves?

The answer is yes. In fact, we have already discussed electrical devices that play roles similar to the roles played by springs and dampers.

Mechanical	Electrical
Damper -- turns mechanical energy into heat. Damping action depends on damping coefficient and motion of the mass that is being damped. F = - b v = - b (Dx/t) In calculus terms: F = - b v = - b (dx/dt)	Resistor -- turns electrical energy into heat. Voltage drop across a resistor depends on resistance and the motion of charge (i.e. current). U = I R = R (DQ/t) In calculus terms: U = I R = R (dQ/dt)
Spring -- stores energy, regardless of whether it is compressed or extended. Energy storage depends on amount of spring deformation, not on motion. F = - k x	Capacitor – stores energy, regardless of which plate carries positive or negative charge. Energy storage depends on amount of charge, not on motion of charge. U = Q/C = (1/C) Q

In this analogy we are building, it appears that there are many analogous quantities:

Mechanical		Electrical
Force (F)	is analogous to	Voltage (U)
Damping coefficient (b)	is analogous to	Resistance (R)
Spring Constant (k)	is analogous to	The inverse of Capacitance (1/C)
Position (x)	is analogous to	Charge (Q)
Velocity (v = Dx/t) (or v = dx/dt in calculus terms)	is analogous to	Current (I = DQ/t) (or I = dQ/dt in calculus terms)

What is missing? Something that plays the role of the mass -- that stores energy due to motion.

Well, for the mass the relevant equations are

F = m a which is F = m (Dv/t)
	In calculus terms this is F = m a = m (dv/dt) = m (d^2x/dt^2)

and

E = ½ m v²

So by analogy we expect this missing electrical factor that is analogous to m (we’ll call the missing factor L) to have the relevant equations of

U = L (DI/t)

In calculus terms this is U = L (dI/dt) = L d^2Q/dt^2

and

E = ½ L I²

This mystery factor L exists. It is called inductance, and it completes our analogy:

Mechanical		Electrical
Force (F)		Voltage (U)
Damping coefficient (b)	F = -bv	Resistance (R)	U = RI
Spring Constant (k)	F = -kx E = ½kx^2	The inverse of Capacitance (1/C)	U = (1/C)Q E = ½(1/C)Q^2
Position (x)		Charge (Q)
Velocity (v = Dx/t)		Current (I = DQ/t)
Mass (m)	F = m(Dv/t) E = ½mv^2	Inductance (L)	U = L(DI/t) E = ½LI^2

Note, our analogy helped us get the equation U = L(DI/t). However, the equation is incomplete, as we will see soon.

Electromagnetic Induction

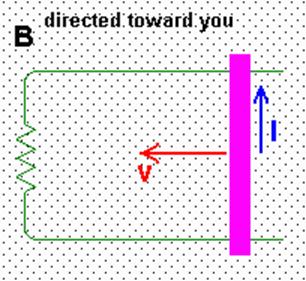
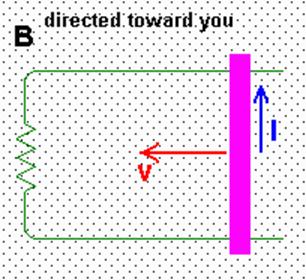What is induction? Consider the picture at right. The purple bar is conducting and is in contact with the green circuit wire.

As the bar moves to the left with speed v, positive charges are forced upward through the bar by the force the B field exerts on them via

F = qv x B

and the Right-Hand-Rule. This creates a current I that runs counter-clockwise through the circuit. Since there is a current, there must be a potential difference (voltage) that appears in the circuit due to the motion of the bar. This is called an induced voltage.

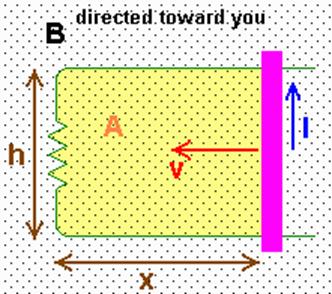In general it is found that current is induced in a circuit any time the magnetic flux through the circuit changes. The magnetic flux F_B is the product of the B-field and the area of the circuit. It can be expressed as a DOT product

F_B = B^.A

where B is the field vector and A is a vector than points perpendicularly to the plane of the circuit and represents the area of the circuit (A = h x in the figure above). However, if the plane of the circuit is perpendicular to the field this is just

F_B = BA

The induced voltage in the circuit is given by the rate of change of the flux

Uinduced = - DFB/t

In calculus terms Uinduced = - dFB/dt

This is known as Faraday’s Law of Induction and it says that any time there is

a change in flux through a circuit, whether it is due to a change in the circuit’s dimensions (as in the case of the purple sliding bar), or

a change in the strength of the B-field, or

a change in the relative orientation of the field and the circuit,

a voltage will be induced in the circuit.

Click here for the induction demo program used in class.

Induction Resists Change

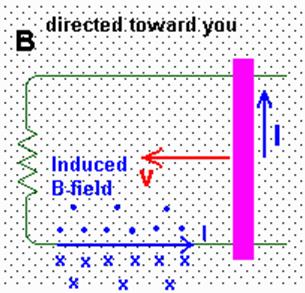
Consider the picture at right again. Because the area of the circuit is decreasing the flux is decreasing. A current is induced in the circuit flowing counter-clockwise.
	The induced current then creates its own magnetic field. This induced field acts to reinforce the existing field -- note the direction of the induced field as given by the Right-Hand-Rule. Therefore, while the motion of the bar decreases the area of the circuit, decreasing the flux, the induced current creates a magnetic field which increases the flux!

In other words, the induction acts to oppose change in flux. If the bar were moved in the opposite direction, the flux would increase. However, the induced current would flow clockwise, creating an induced field that opposed the existing B field and hence decreasing the flux.

It is a general rule that induction always acts to oppose change. That is why there is a negative sign in Faraday’s Law. The “induction always acts to oppose change” rule is known as Lenz’s Law.

Inductance

The connection between Faraday’s Law and the inductance “L” value that we arrived at earlier is fairly easy to see in the case of a solenoid.

A while back we discussed solenoids. We learned that the magnetic field created by a solenoid is

Solenoid viewed from side.

Where K_m is called the relative permeability of the material in the core of the solenoid, N is the number of turns in the solenoid, l is the length of the solenoid, I is the current through the solenoid, and m₀ is the permeability of free space.

The flux through a solenoid then is

Where A is the cross-sectional area of the solenoid. The N term shows up because there is flux through each loop in the solenoid.

Solenoid viewed from end.

Combining our equations for magnetic field and flux we get

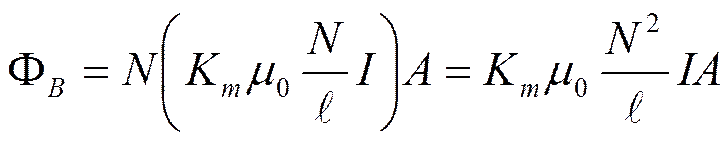
Note – in the discussion below, non-calculus versions of the equations are on the left; calculus versions are on the right highlighted in yellow. So long as the current flowing through the solenoid is steady, no voltage is induced. However, if the current is changed, the Faraday’s Law kicks in:
Among all these terms, only the current varies. The rest are all either the dimensions of the solenoid or physical constants:
The quantity in brackets is the inductance L of the solenoid
and the induced voltage is

The negative sign, which we did not have in our earlier derivation of inductance by analogy, indicates that Lenz’s Law is present in the solenoid – the induced voltage always acts to oppose change in current.

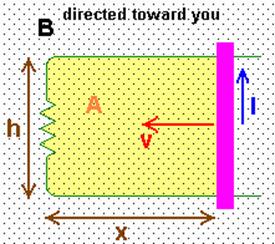Example Problem #1

In the picture at left, h = 5 cm, x = 7 cm, the bar is moving to the left at v = 10 m/s, B = 5 T directed perpendicular the plane of the circuit, and the resistance in the circuit is 0.1 W.

a) Calculate the magnetic flux.

b) Calculate the current induced in the circuit.

c) Calculate the force required to move the bar at that speed.

Solution:

A = .05 m x .07 m = .0035 m²

B = 5 T

F_B = BA = 5 T (.0035 m²) = 0.0175 Tm²

The flux is 0.0175 Tm².

Now let’s get the induced current. First I’ll figure the induced voltage:

U_induced = - DF_B/t

= - B(DA/t)

A = hx so this is now

V_induced = - Bh(Dx/t)

= - Bhv

= - 5 T (.05 m) (10 m/s)

= - 2.5 Tm²/s

Let me work out the units on that:

[T]m²/s = [N/Am]m²/s = [N/A]m/s = (Nm)/(As) = J/C = Volt

So, keeping in mind the fact that the negative sign just indicates that induction opposed change, the induce voltage in the circuit is 2.5 V.

So the current induced is

I_induced = V_induced/R = 2.5 V/0.1 W = 25 A

25 A of induced current appear in the circuit.

What about the force F required to move the bar at v = 10 m/s?

Well, I know from Physics I that

F v = Power

I also know that in a circuit

Power = I V

The power from the force must be what goes into making current flow in the circuit, so

F v = I V

F (10 m/s) = (25 A)(2.5 V)

F (10 m/s) = 62.5 VA = 62.5 [J/C][C/s]

F (10 m/s) = 62.5 J/s

F = 6.25 J/m = 6.25 Nm/m = 6.25 N

It takes 6.25 N of force to move the bar. It takes work to generate electric current!

Example Problem #2

Inductance is measured in units of Henrys. What is a Henry, in terms of more basic units?

Solution:

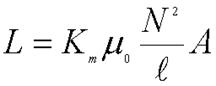
N has no units – it is just a number. Ditto for K_m. The SI units for A would be m². m₀ has units of Tm/A according to one book I looked up the value in, N/A² according to another. l is measured in m. We’ll work out both versions:

Version with Tm/A	Version with N/A^2

So it seems a Henry is a Joule per square Ampere.

Example Problem #3

A solenoid has diameter 5 cm, length 100 cm, and contains 10,000 turns of wire. It has a core with relative permeability 1000. Find the inductance of this solenoid. What voltage will be induced on it if current through the solenoid increases at a rate of 2 A per minute?

Solution:

	I gather together my information and plug it into the inductance equation for a solenoid. Since I just worked out the units for this in the previous example, I’m leaving units out.
	The rate of change of the current is 2 A in one minute.
	I’ll work through these units.
And my final answers are that the solenoid has an inductance of 247 H and when current is increased through it at a rate of 2 A/min, an induced voltage of 8.2 V appears across the inductor.