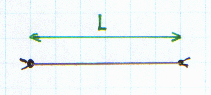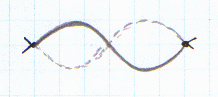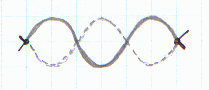DAY 18

Summary of Topics Covered in Today’s Lecture

NOTE – THIS PAGE USES A LOT OF ANIMATION, AND CONTAINS SUB-PAGES.

IT WILL NOT PRINT VERY WELL.

Standing Waves

Waves tend to be reflected by changes in the medium through which they travel. In many systems in which the medium has definite boundaries such as…

q a string clamped on both ends (like a guitar or cello string)

q a pipe containing air (like a flute or organ pipe)

q a drinking glass or wire hoop or bell

…waves being reflected from the boundaries in the system can interfere with other waves in the system to create fixed patterns known as standing waves.

Click here for an animation that shows how two waves can interfere to create a standing wave.

The points of zero amplitude motion in a standing wave are called nodes. The points of maximum amplitude motion are called antinodes.

A standing wave on a string that is clamped at both ends is bound by the limits of the string, so only certain wavelengths of standing waves can exist.

Consider a piece of string of length L clamped on each end. Because of the clamps, the only standing waves that can exist on this string are those that have nodes at each end. Those are boundary conditions for this system.
The longest wavelength standing wave that can exist under these boundary conditions is one that has a node at each end and one antinode, as pictured at right. Only half of a full wave cycle appears here, so the wavelength of the standing wave is two times the length of the string. Wavelength: l = 2L Number of antinodes: n = 1 This is called the fundamental vibration of this string.
The second longest wavelength standing wave that can exist is one that has a node at each end and two antinodes. A full wave cycle appears here, so the wavelength of the standing wave is simply the length of the string. Wavelength: l = L Number of antinodes: n = 2 This is called the second harmonic vibration of this string.
The third longest wavelength standing wave that can exist is one that has a node at each end and three antinodes. A full wave cycle, plus half of another cycle, appears here. The wavelength of the standing wave is 2/3 the length of the string. Wavelength: l = 2/3 L Number of antinodes: n = 3 This is called the third harmonic vibration of this string.

There are theoretically an infinite number of harmonics. Note that the nth harmonic has n antinodes and a wavelength of

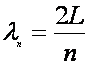
The frequency of the nth harmonic is given by f l = v (where v is the speed of the wave).

The frequency of the fundamental (n=1) is

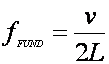
So the harmonic frequencies are all integer multiples of the fundamental.

The wavelengths and frequencies of standing waves are quantized. If a vibrating string has fundamental frequency of 100 Hz, then standing waves of 200 Hz, 300 Hz, 400 Hz, etc. are possible. But there are no standing waves at 215 Hz, or 350 Hz, etc.

While the details differ from system to system, it is possible to create standing waves in many different kinds of systems, from a hoop of wire to the head of a drum.

http://pirt.asu.edu/detail_3.asp?ID=1924&offset=75

http://physics.usask.ca/~hirose/ep225/animation/drum/anim-drum.htm These images are animated – wait for them to load.
However, string, hoop, drum, or whatever – the equation

always holds. The Harmonic frequencies are always integer multiples of the fundamental frequency.

All standing wave frequencies (all fn) are natural frequencies of whatever object is supporting the standing waves. That means it is possible to achieve resonance at any standing wave frequency. Probably the most famous example of standing waves and resonance in action is the collapse of the Tacoma Narrows Bridge. A standing wave formed on the bridge (visible in the picture – a node exists at each tower and in the center of the span; two antinodes are present; this appears to be a 2nd harmonic-type wave) and the large-amplitude oscillations due to resonance tore the bridge apart. The following links are to YouTube videos on the Tacoma Narrows collapse: Old B&W footage (click here) Color footage (click here) Excellent short film on the bridge, the cause of its collapse, and how the collapse led to improvements in bridge building (click here)

http://www.lib.washington.edu/specialcoll/exhibits/tnb/fall5b5.jpg

Example Problem #1

Sound travels at roughly 340 m/s. A tube that is open on both ends has a fundamental with a wavelength twice the length of the tube. Determine the frequency of the fundamental and first three harmonics of an open-ended tube 2 m long.

Solution:

L = 2 m

l_FUND = 4 m

f_FUND = v/l_FUND

f_FUND = 340 m/s / 4 m = 85 1/s = 85 Hz

f_n = n f_FUND

f_FUND = 85 Hz

f₂ = 2 (85 Hz) = 170 Hz

f₃ = 3 (85 Hz) = 255 Hz